Question

In a set of 25 aluminum castings, four castings are defective (D), and the remaining twenty-one are good (G). A quality control inspector randomly selects three of the twenty-five castings without replacement to test. The sample space for selecting the group to test contains ____________ elementary events.

Answer 1

The sample space for selecting the group to test contains 2,300 elementary events.

Explanation:

There are a total of N = 25 aluminum castings.

Of these 25 aluminum castings, n₁ = 4 castings are defective (D) and n₂ = 21 are good (G).

It is provided that a quality control inspector randomly selects three of the twenty-five castings without replacement to test.

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!(n-k)!)`

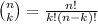
Compute the number of samples that are possible as follows:

`{25\choose 3}=(25!)/(3!* (25-3)!)`

`=(25* 24* 23* 22!)/(3!* 22!)\\\\=(25* 24* 23)/(3* 2* 1)\\\\=2300`

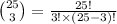
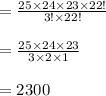
The sample space for selecting the group to test contains 2,300 elementary events.