Question

what is the probability that a measurement of the energy at time t will yield the result h^2pi^2/2ml^2

Answer 1

The probability is
`(1)/(2)`

Step-by-step explanation:

Given that,

The energy at time t will yield the result
`h^2pi^2/2ml^2`

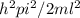
Suppose, At time t = 0 the normalized wave function for a particle of mass m in the one-dimensional infinite well is given by,

`V(x)={0 0<x<L,\ \infty\ elsewhere`

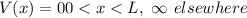
The normalized wave function is,

`\psi(x)=(1+i)/(2)\sqrt{(2)/(L)}\sin(\pi x)/(L)+(1)/(√(2))\sqrt{(2)/(L)}\sin(2\pi x)/(L)\ 0<x<L, 0\ elsewhere`

What is the probability that a measurement of the energy at time t will yield the result h^2 pi^2/2mL^2?

We need to find the probability

Using given data

`probability=((1+i)/(2))((1-i)/(2))`

`probability=(1-i^2)/(4)`

`probability=(1+1)/(4)`

`probability=(1)/(2)`

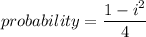
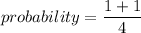
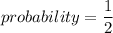
Hence, The probability is
`(1)/(2)`