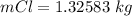Question

Consider the rechargeable battery: Zn(s)0ZnCl (aq)7Cl2(aq)0Cl (l)0C(s) (a) Write reduction half-reactions for each electrode. From which electrode will electrons flow from the battery into a circuit if the electrode potentials are not too different from E 8 values

Answer 1

Complete Question

Consider the rechargeable battery:
`Zn(s)||ZnCl _((aq))||Cl_2_((aq))|Cl_2 (l)|C_((s))`

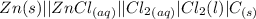
(a) Write reduction half-reactions for each electrode. From which electrode will electrons flow from the battery into a circuit if the electrode potentials are not too different from
`E^o` values

(b)

if the battery delivers a constant current of
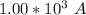`1 .00 *10^(3) \  A` for 1.00 h , how many kg of
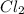`Cl_2` will be consumed

Answer:

a

At the anode

`Zn^(2+) + 2e^(-)  \to  Zn_(s) \ \ \  E^o  =  -0.762 V`

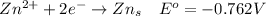
At the cathode

`Cl_2 _((l)) +  2e^(-)  \to 2Cl^(-) _(aq) \ \ \ \ E^o =  1.396 V`

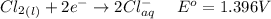
b

The value is
`mCl  =  1.32583 \ kg`

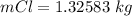
Step-by-step explanation:

Generally the half-reactions for each electrode is mathematically represented as

At the anode

`Zn^(2+) + 2e^(-)  \to  Zn_(s) \ \ \  E^o  =  -0.762 V`

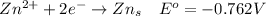
At the cathode

`Cl_2 _((l)) +  2e^(-)  \to 2Cl^(-) _(aq) \ \ \ \ E^o =  1.396 V`

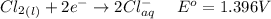
Generally from the question we are told that

The current is
`I =  1.00 *10^(3) \ A`

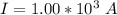
The time is
`t =  1.00\  h= 3600`

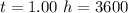
Generally the quantity of charge consumed is

`Q = It`

=>
`Q = 1.00 *10^(3) *  3600`

=>
`Q = 3.6 *10^(6) \  C`

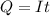
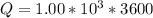
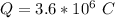
Generally the number of moles of electron consumed is

`n =  (Q)/(F)`

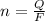
Here F is the faradays constant with value
`F =  (96500C/mole \ e-)`

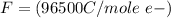
So

`n =  ( 3.6 *10^(6) )/(96500)`

=>
`n = 37.3 \  moles`

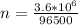
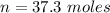
Generally the number of moles of
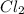`Cl_2` consumed is mathematically represented as

`nCl = (1)/(2)  * n`

=>
`nCl = (1)/(2)  * 37.3`

=>
`nCl = 18.7 \  moles`

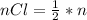
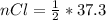
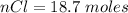
Generally the mass of
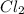`Cl_2` consumed is mathematically represented as

`mCl  =  nCl  *  Z`

Here Z is the molar mass of
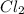`Cl_2` is Z = 70.9 g/mole

So

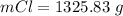
`mCl  =  18.7  *  70.9`

=>
`mCl  =  18.7  *  70.9`

=>
`mCl  =  1325.83 \ g`

=>
`mCl  =  1.32583 \ kg`