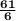Question

What is the sum of zeros of the equation (m-10)(6m-1)=0. Ancwer your question as a fraction

PLSSS SOMEONE ANCWEE THISS BEGGINGG.​

Answer 1

The sum of zeros is
`(61)/(6)`

Explanation:

The Rule of Zero Product

The rule of zero product states that the product of two nonzero elements is nonzero. It can be written as the following assertion:

If a.b=0, then a=0 or b=0

The equation

(m-10)(6m-1)=0

can be solved by applying the mentioned rule:

`m-10=0 \ \ \Rightarrow m=10`

`6m-1=0 \ \ \Rightarrow m=1/6`

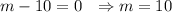
The sum of both solutions is:

`\displaystyle 10+(1)/(6)=(61)/(6)`

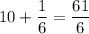
The sum of zeros is
`\mathbf{(61)/(6)}`