Answer:
4/7
Explanation:
Using the hint, we have an original fraction of x/(x+3). The given manipulations and relations can be used to find the value of x, and the original fraction.
__
adding 2 to each term
The new fraction is ...
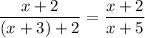
new value
Apparently, the new value of this fraction is 2/3. We can use this to find the value of x.

The original fraction is ...
4/(4+3) = 4/7
_____
Alternate solution
In the ratio 2/3, the numerator is twice the difference between the denominator and numerator. 2 = 2(3 -2)
The problem statement tells us the difference between the numerator and denominator is 3. That is not changed by adding the same number to each. This means the fraction equivalent to 2/3 is (2·3)/(3·3) = 6/9. Subtracting 2 from each of the numerator and denominator gives the original fraction:
(6-2)/(9-2) = 4/7