Question

I NEED HELP SOLVING THIS!!!!!!!!!!!!

Jose Altuve hits a fastball with a velocity of 49.1 m/s (109.9 mph) at an angle of 22º. If left field is 96 m (315 ft) away, will this be a home run?

Answer 1

Yes

Step-by-step explanation:

The given parameters are;

The speed with which the fastball is hit, u = 49.1 m/s (109.9 mph)

The angle in which the fastball is hit, θ = 22°

The distance of the field = 96 m (315 ft)

The range of the projectile motion of the fastball is given by the following formula

`Range = (u^2 * sin(2\cdot \theta))/(g)`

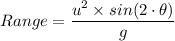
Where;

g = The acceleration due to gravity = 9.81 m/s², we have;

`Range = (49.1^2 * sin(2*22^(\circ)))/(9.81) \approx 170.71 \ m`

Yes, given that the ball's range is larger than the extent of the field, the batter is able to safely reach home.