Answer:
Correct Choice: Second Option
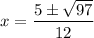
Explanation:
Standard Form of Quadratic Function
The standard representation of a quadratic function is:
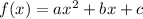
where a,b, and c are constants.
Solving with the quadratic formula:
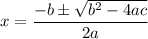
We have the following equation to solve:
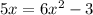
Rearranging all the terms to the left side:
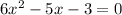
Comparing with the general form of the quadratic equation: a=6, b=-5, c=-3. Apply the formula:
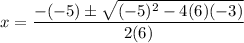
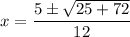
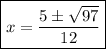
Correct Choice: Second Option