Answer:
x = 9
Explanation:
Given equation:
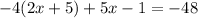
Apply distributive property rule: x(y + z) = xy + xz
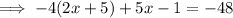
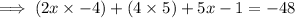
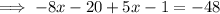
Combine like terms on the left hand side to simplify the expression:
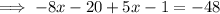
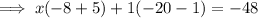
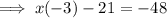
Add 21 on both sides to remove all the mathematical operations (addition, subtraction, multiplication, division) being performed on the L.H.S

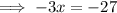
Cancel the "-" by dividing "-1" both sides:
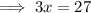
Divide 3 on both sides to isolate the coefficient from x.
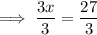

Check:
Now, let's check our answer. This can be done by substituting the obtained value of "x", into the given equation and simplifying it.
Correct/Incorrect:
If L.H.S = R.H.S, then the value of "x" is correct.
If L.H.S ≠ R.H.S, then we might have to recheck our work we did above.
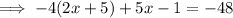
Plugging x = 9 into the equation:
![\implies -4[2(9) + 5] + 5(9) - 1 = -48](https://img.qammunity.org/2023/formulas/mathematics/college/meo4okx0t996u2ym55zfzs1aw28kqa3p52.png)
Simplifying the expression using PEMDAS:
![\implies -4[18 + 5] + 5(9) - 1 = -48](https://img.qammunity.org/2023/formulas/mathematics/college/bweiu69sd358npasmxov8twk0wrgmofl4j.png)
Simplifying the expression inside the parentheses (18 + 5) and evaluating the product of 5 and 9:
![\implies -4[23] + 45 - 1 = -48](https://img.qammunity.org/2023/formulas/mathematics/college/33bj960epc8qwn903npigbhnq52t25qngk.png)
Opening the parentheses "-4[23]" and multiplying -4 and 23

Subtracting 45 both sides of the equation:
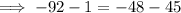

Simplifying the L.H.S:
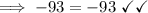
Therefore, our answer is correct.