Question

-4(2x + 5) + 5x - 1 = - 48

Answer 1

x = 9

Explanation:

Given equation:

`-4(2x + 5) + 5x - 1 = -48`

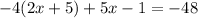
Apply distributive property rule: x(y + z) = xy + xz

`\implies -4(2x + 5) + 5x - 1 = -48`

`\implies (2x * -4) + (4 * 5) + 5x - 1 = -48`

`\implies -8x - 20 + 5x - 1 = -48`

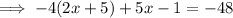
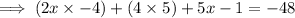
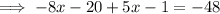
Combine like terms on the left hand side to simplify the expression:

`\implies -8x - 20 + 5x - 1 = -48`

`\implies x(-8 + 5) + 1(-20 - 1) = -48`

`\implies x(-3) - 21 = -48`

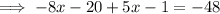
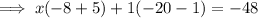
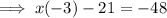
Add 21 on both sides to remove all the mathematical operations (addition, subtraction, multiplication, division) being performed on the L.H.S

`\implies-3x + 21 - 21 = -48 + 21`

`\implies -3x = -27`

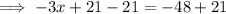
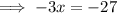
Cancel the "-" by dividing "-1" both sides:

`\implies 3x = 27`

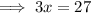
Divide 3 on both sides to isolate the coefficient from x.

`\implies (3x)/(3) = (27)/(3)`

`\implies \boxed{x = 9}`

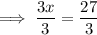
Check:

Now, let's check our answer. This can be done by substituting the obtained value of "x", into the given equation and simplifying it.

Correct/Incorrect:

If L.H.S = R.H.S, then the value of "x" is correct.

If L.H.S ≠ R.H.S, then we might have to recheck our work we did above.

`\implies -4(2x + 5) + 5x - 1 = -48`

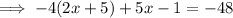
Plugging x = 9 into the equation:

`\implies -4[2(9) + 5] + 5(9) - 1 = -48`

Simplifying the expression using PEMDAS:

`\implies -4[18 + 5] + 5(9) - 1 = -48`

Simplifying the expression inside the parentheses (18 + 5) and evaluating the product of 5 and 9:

`\implies -4[23] + 45 - 1 = -48`

Opening the parentheses "-4[23]" and multiplying -4 and 23

`\implies -92 + 45 - 1 = -48`

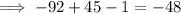
Subtracting 45 both sides of the equation:

`\implies -92 - 1 = -48 - 45`

`\implies -92 - 1 = -93`

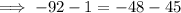
Simplifying the L.H.S:

`\implies -93 = -93 \ \checkmark \checkmark`

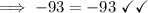
Therefore, our answer is correct.

Answer 2

`\tt x=9`

Explanation:

`\tt -4(2x + 5) + 5x - 1 = - 48`

Apply the distributive property to multiply -4 by 2x+5:-

`\tt -8x-20+5x-1=-48`

Combine like terms:-

`\tt -3x-21=-48`

Add 21 to both sides:-

`\tt -3x=-48+21`

`\tt -3x=-27`

Divide both sides by -3:-

`\tt \: x = \cfrac{ - 27}{ - 3}`

`\tt x=9`

Hope this answers your question!