Question

To find the slope of the two points

Answer 1

Slope is :-

`\boxed{\bf \; m \; = - \cfrac{7}{5}}`

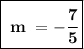
Explanation:

Given two points :-

`\sf \implies(-5,3) , (0,−4)`

To Find :-

The slope of Two points that is given.

Solution :-

`\sf \implies(-5,3) , (0,−4)`

As we know that the formula of Slope is :-

`\sf \implies \boxed{\sf Slope = \cfrac {y_2 - y_1}{x_2 - x_1}}`

Now, Put the values of x and y :-

Where,

`{ \sf \: {y_2} = - 4}`

`\sf \: x_2 = 0`

`\sf \: y_1 = 3`

`\sf \: x_1 = - 5`

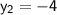
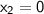
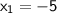
Put the values on their respective place :-

`\sf \implies \: Slope = \cfrac{ - 4 - 3}{0 - ( - 5)}`

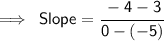
Simplify this Fraction :-

Add -4 and -3 which is on the numerator as we know that "-" and "-" equals to "+":-

`\sf \implies \: Slope = \cfrac{ - 7}{0 - ( - 5)}`

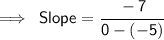
Now Add 0-(-5) on the denominator as we know that "-" and "-" equals to "+":-

`\sf \implies \: Slope = \: \cfrac{ - 7}{ 5}`

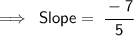
Which can be rewritten as,

`\sf \implies \: m = \: - \cfrac{7}{5}`

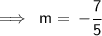
This fraction can't be cancelled. Hence, the slope of the two points is:-

`\sf \implies \boxed{\sf m = \: - \cfrac{7}{5}}`

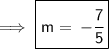
Note :- Slope can also be denoted as
`m`.

________________________________

I hope this helps!