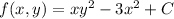It looks like the vector field is
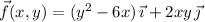
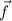 is conservative if we can find a scalar function
is conservative if we can find a scalar function
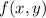 whose gradient is
whose gradient is
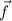 . This entails solving the partial differential equations
. This entails solving the partial differential equations
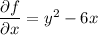
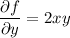
Integrate both sides of the second PDE with respect to y :
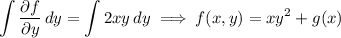
Differentiate with respect to x and solve for
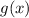 :
:
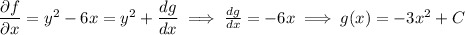
It follows that
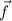 is indeed conservative with potential function
is indeed conservative with potential function