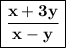Question

Hi.

Please i need help with these questions :

Simplify
1.

`\frac{ {d}^(2) - 9 }{ {d}^(2) - 7d + 12 }`
2.

`\frac{ {m}^(2) + 2mn + {n}^(2) }{ {m}^(2) - {n}^(2) }`
3.

`\frac{ {x}^(2) + xy - 6 {y}^(2) }{ {x}^(2) - 3xy + 2 {y}^(2) }`
​

Answer 1

1)

`(d^2 - 9)/(d^2 - 7d + 12) = ((d - 3)(d + 3))/((d - 3)(d - 4)) = (d + 3)/(d - 4)`

2)

`(m^2 + 2mn + n^2)/(m^2 - n^2) = ((m + n)(m + n))/((m - n)(m + n)) = (m + n)/(m - n)`

3)

`(x^2 + xy - 6y^2)/(x^2 - 3xy + 2y^2) = ((x + 3y)(x - 2y))/((x - y)(x - 2y)) = (x + 3y)/(x - y)`

Answer 2

Solutions :

1.
`\bf \frac{ {d}^(2) - 9 }{ {d}^(2) - 7d + 12 }`

`\tt : \implies \frac{ {d}^(2) - (3)^(2) }{ {d}^(2) - 3d - 4d + 12 }`

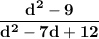
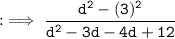
By using identinty a² - b² = (a + b)(a - b) in numerator and splitting method in denominator :

`\tt : \implies \frac{ (d+3)(d-3) }{ {d}^(2) - 3d - 4d + 12 }`

`\tt : \implies ( (d+3)(d-3) )/(d(d - 3) - 4(d - 3))`

`\tt : \implies \frac{ (d+3)\cancel{(d-3)} }{\cancel{(d - 3)}(d - 4)}`

`\tt : \implies (d+3)/(d - 4)`

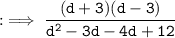
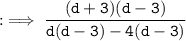
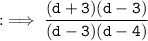
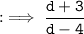
Hence, answer is
`\boxed{\bf (d+3)/(d - 4) }`

________________________________

2.
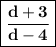
`\bf \frac{ {m}^(2) + 2mn + {n}^(2) }{ {m}^(2) - {n}^(2) }`

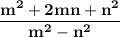
By using identinty a² + 2ab + b² = (a + b)² in numerator and a² - n² = (a + b)(a - b) in denominator :

`\tt : \implies ((m+n)^(2))/((m+n)(m-n))`

`\tt : \implies \frac{\cancel{(m+n)}(m+n)}{\cancel{(m+n)}(m-n)}`

`\tt : \implies (m+n)/(m-n)`

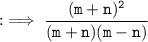
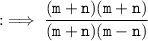
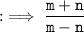
Hence, answer is
`\boxed{\bf (m+n)/(m-n)}`

________________________________

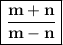
3.
`\bf \frac{{x}^(2) + xy - 6{y}^(2)}{{x}^(2) - 3xy + 2{y}^(2)}`

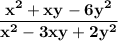
By using splitting method in both numerator and denominator :

`\tt : \implies \frac{{x}^(2) + 3xy - 2xy - 6{y}^(2)}{{x}^(2) - xy - 2xy + 2{y}^(2)}`

`\tt : \implies (x(x + 3y) - 2y(x + 3y))/(x(x - y) - 2y(x - y))`

`\tt : \implies \frac{\cancel{(x-2y)}(x + 3y)}{\cancel{(x-2y)}(x - y)}`

`\tt : \implies (x + 3y)/(x - y)`

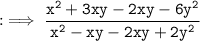
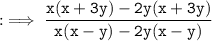
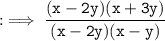
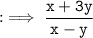
Hence, answer is
`\boxed{\bf (x + 3y)/(x - y)}`