Answer:
 is
is
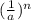 OR
OR
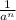
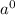 = 1, where a ≠ 0
= 1, where a ≠ 0
Explanation:
To simplify the exponents, you must put it in positive value
Example:
The simplest form of
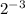 is to change the exponent from negative value to positive value.
is to change the exponent from negative value to positive value.
- You can do that by reciprocal the number,
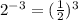
- You can write it
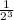 , because 1 to any power equal 1
, because 1 to any power equal 1
That means if you want to simplify
 , reciprocal a and change the sign of the power from -n to n
, reciprocal a and change the sign of the power from -n to n
The simplest form of
 is
is
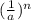 OR
OR
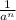
For any number, a (a ≠ 0), 1 × a = a, so, the reason that any number to the zero power is 1 because any number to the zero power is just the product of no numbers at all, which is the multiplicative identity, (1)
Example:
The value of
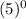 = 1, because it is the product of no numbers, so it is equal to the multiplicative identity (1)
= 1, because it is the product of no numbers, so it is equal to the multiplicative identity (1)
That means
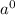 = 1, where a ≠ 0
= 1, where a ≠ 0
Very important note:
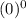 is undefined value
is undefined value