Question

A van slows down uniformly from 17 m/s to 0 m/s in 5 s. How far does it travel before stopping?

Procedure is required.

Answer 1

Before stopping, the van travels 42.5 m

Step-by-step explanation:

Constant Acceleration Motion

It's a type of motion in which the velocity of an object changes by an equal amount in every equal period of time.

Being a the constant acceleration, vo the initial speed, vf the final speed, and t the time, the following relation applies:

`v_f=v_o+at\qquad\qquad [1]`

The distance traveled by the object is given by:

`\displaystyle x=v_o.t+(a.t^2)/(2)\qquad\qquad [2]`

The van slows down uniformly from v0=17 m/s to vf=0 m/s in t=5 s. The acceleration can be calculated by solving [1] for a:

`\displaystyle a=(v_f-v_o)/(t)`

`\displaystyle a=(0-17)/(5)=-3.4\ m/s^2`

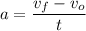
The distance covered is:

`\displaystyle x=17\cdot 5+((-3.4)\cdot 5^2)/(2)`

`\displaystyle x=85-42.5=42.5`

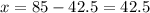
Before stopping, the van travels 42.5 m