Answer:
Explanation:
A). g(x) = x² - 9x + 14
Since coefficient of highest degree term (x²) is positive, parabola will open upwards.
For any parabola opening upwards,
Right end behavior,
y → ∞ as x → ∞
B). Let the equation of the linear function is,
f(x) = mx + b
Where m = slope of the function
b = y-intercept
From the graph attached,
Slope 'm' =
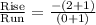
m = -3
b = -1
Therefore, function 'f' will be,
f(x) = (-3)x - 1
f(x) = -3x - 1
g(x) = x² - 9x + 14
= x² - 7x - 2x + 14
= x(x - 7) - 2(x - 7)
= (x - 2)(x - 7)
If h(x) = f(x)g(x)
h(x) = -(3x + 1)(x -2)(x - 7)
For h(x) ≥ 0
-(3x + 1)(x - 2)(x - 7) ≥ 0
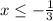 Or 2 ≤ x ≤ 7
Or 2 ≤ x ≤ 7
Therefore, for 2 ≤ x ≤ 7, h(x) ≥ 0
C). If k(x) =
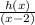
k(x) =
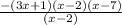
k(x) = -(3x + 1)(x - 7)
For k(x) = -56
-(3x + 1)(x - 7) = -56
3x² -20x - 7 = 56
3x² - 20x - 63 = 0
3x² - 27x + 7x - 63 = 0
3x(x - 9) + 7(x - 9) = 0
(3x + 7)(x - 9) = 0
