Question

1. Let f(x) be defined by the linear function graphed below and

g(x) = x2 - 9x + 14.
I
A. Describe the right end behavior of g(x).

Answer 1

Explanation:

A). g(x) = x² - 9x + 14

Since coefficient of highest degree term (x²) is positive, parabola will open upwards.

For any parabola opening upwards,

Right end behavior,

y → ∞ as x → ∞

B). Let the equation of the linear function is,

f(x) = mx + b

Where m = slope of the function

b = y-intercept

From the graph attached,

Slope 'm' =
`\frac{\text{Rise}}{\text{Run}}=(-(2+1))/((0+1))`

m = -3

b = -1

Therefore, function 'f' will be,

f(x) = (-3)x - 1

f(x) = -3x - 1

g(x) = x² - 9x + 14

= x² - 7x - 2x + 14

= x(x - 7) - 2(x - 7)

= (x - 2)(x - 7)

If h(x) = f(x)g(x)

h(x) = -(3x + 1)(x -2)(x - 7)

For h(x) ≥ 0

-(3x + 1)(x - 2)(x - 7) ≥ 0

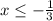`x\leq -(1)/(3)` Or 2 ≤ x ≤ 7

Therefore, for 2 ≤ x ≤ 7, h(x) ≥ 0

C). If k(x) =
`(h(x))/((x-2))`

k(x) =
`(-(3x+1)(x-2)(x-7))/((x-2))`

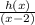
k(x) = -(3x + 1)(x - 7)

For k(x) = -56

-(3x + 1)(x - 7) = -56

3x² -20x - 7 = 56

3x² - 20x - 63 = 0

3x² - 27x + 7x - 63 = 0

3x(x - 9) + 7(x - 9) = 0

(3x + 7)(x - 9) = 0

`x=-(7)/(3),9`