The question is incomplete. Here is the complete question.
The rectangle bleow has an area of
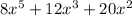 . The width of the rectangle is equal to the greatest common monomial factor of
. The width of the rectangle is equal to the greatest common monomial factor of
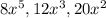 . What is the length and width of the rectangle?
. What is the length and width of the rectangle?
Answer: width =
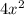
length =

Explanation: Greatest common factor is the largest number that will divide into that number without rest, i.e., it's a number that will result in an exact division. The same can be applied to a polynomial.
To find the greatest common factor:
1) Write each in prime factored form:
2.2.2.x.x.x.x.x + 2.2.3.x.x.x + 2.2.5.x.x
2) Identify the common factor among the terms:
For this polynomial, the repetitive factor is
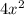
Therefore, the width of the rectangle is:
w =
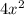
Area of a rectangle is the multiplication of width and length, so:
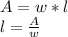
To calculate length, we will have to divide polynomials:
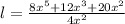

Width and length of the rectangle are 4x² and
 , respectively.
, respectively.