Answer:
The probability that the product will be successfully launched given that the market test result comes back negative is 0.30.
Explanation:
Denote the events provided as follows:
S = a product is successfully launched
P = positive test market result
The information provided is:
P (S) = 0.60
P (P | S) = 0.80
P (P | S') = 0.30
Then,
P (P' | S) = 1 - P (P | S) = 1 - 0.80 = 0.20
P (P' | S') = 1 - P (P | S') = 1 - 0.30 = 0.70
Compute the probability of positive test market result as follows:
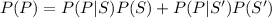

The probability of positive test market result is 0.60.
Then the probability of negative test market result is:
P (P') = 1 - P (P)
= 1 - 0.60
= 0.40
Compute the probability that the product will be successfully launched given that the market test result comes back negative as follows:

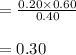
Thus, the probability that the product will be successfully launched given that the market test result comes back negative is 0.30.