Answer: 1.2 hours
Explanation:
Given: : Time taken by Julius to complete the job alone:
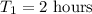
Time taken by Marcos to complete the job alone :
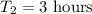
Let the time taken by both to complete the job together = T
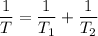

Hence, it will take 1.2 hours to complete the job by working together.