Question

Sara pays $4.50 for 3 pounds of bananas and 2 pounds of oranges. One pound of oranges costs $0.75 more than one pound of bananas. Let b represent the price per pound of bananas. What equation represents the situation, and what is the price per pound of each fruit?

Answer 1

The price of one pound of banana = b

As one pound of oranges costs $0.75 more than one pound of bananas, so, the price of one pound of orange = b+0.75.

The price of 3 pounds of banana = 3b,

and the price of 2 pounds of oranges = 2(b+0.75).

Now, as she pays $4.50 for 3 pounds of bananas and 2 pounds of oranges.

So, for this situation the required equation is

3b + 2(b+0.75) =4.5

On solving this equation, we have

`\Rightarrow 3b+2b+2*0.75=4.5`

`\Rightarrow 5b +1.5=4.5`

`\Rightarrow 5b =4.5-1.5=3`

`\Rightarrow b =\frac 3 5=0.6`

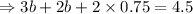
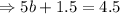
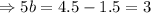
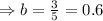
Hence, the price of one pound of banana = $ 0.60

and the price of one pound of orange

=b+0.75= 0.60+0.75=$1.35.