Question

Wholemark is an Internet order business that sells one popular New Year greeting card once a year. The cost of the paper on which the card is printed is $0.40 per card, and the cost of printing is $0.10 per card. The company receives $3.75 per card sold. Since the cards have the current year printed on them, unsold cards have no salvage value. Their customers are from the four areas: Los Angeles, Santa Monica, Hollywood, and Pasadena. Based on past data, the number of customers from each of the four regions is normally distributed with mean 2,300 and standard deviation 200. (Assume these four are independent.)

What is the optimal production quantity for the card?

Answer 1

9644

Step-by-step explanation:

cost of paper on which a card is printed = $0.40 per card

cost of printing = $0.10 per card

profit made per card sold = $3.75

number of areas where customers are located (n)= 4

mean of customers from each region = 2300

standard deviation for each region = 200

note : each region is independent

The optimal production quantity for the card can be calculated going through these steps

first we determine

the cost of card = $0.10 + $0.40 = $0.50

selling value = $3.75

salvage value = 0

next we calculate for the z value

= ( selling value - cost of card) / ( selling price - salvage value )

= ( 3.75 - 0.50 ) / 3.75 = 0.8667

Z( 0.8667 ) = 1.110926 ( using excel formula : NORMSINV ( 0.8667 )

next we calculate

u = n * mean demand

= 4 * 2300 = 9200

б =
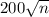`200√(n)` = 200 * 2

= 400

Hence optimal production quantity for the card

= u + Z (0.8667 ) * б

= 9200 + 1.110926 * 400

= 9644.3704

≈ 9644