Answer:
f(x) is continuous on the interval [0, 1], f(0) = -2 , and f(1) = 1.718 . Since f(0) < 0 < f(1) , there is a number c in (0, 1) such that f(c) = 0 by the Intermediate Value Theorem. Thus, there is a root of the equation ex = 3 − 2x, in the interval (0, 1)
Explanation:
From the question we are told that
The equation is
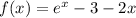
The interval is [0, 1]
Generally f(0) is
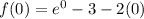
=>

=>
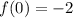
Generally f(1) is



From the value we see that at x = 0 , f(0) = -2 which is below the x-axis
and the at x = 1 , f(1) = 1.718 which is above the x-axis
Now the according to Intermediate Value Theorem , given the condition stated above, there will exist a root c in the interval such that
f(c) = 0