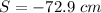Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The position of the emitter is
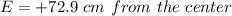
The position of the stone is
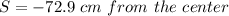
Explanation:
From the question we are told that
The length is l = 178 cm
The width is w = 102 cm
Generally the position of the stone along the horizontal axis is mathematically evaluated as
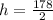
=>
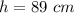
Generally the position of the emitter along the vertical axis is mathematically evaluated as
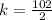
=>
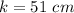
Generally the resultant position of both stone and the emitter is
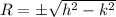
=>

=>
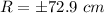
Hence the position of the emitter is
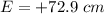
the position of the stone is