Question

Suppose a boat moves at 12.0m/s relative to the water. If the boat is in a river with the current directed east of 2.50m/s, what is the boat's speed relative to the groiund when it is heading (a) east, with the current, and (b) west, against the current?

Answer 1

(a) 14.5 m/s

(b) 9.5 m/s

Step-by-step explanation:

Let the speed of the boat in the still water (i.e relative to ground) is
`v_0`.

Given that the speed of the boat relative to water,
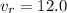`v_r=12.0` m/s.

Speed of the water current of the river relative to the ground,
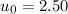`u_0=2.50` m/s towards east.

(a) When the boat is heading toward the east (in the same direction of the current of the river)

The relative velocity,
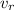`v_r`, of the boat with respect to ground is

`v_r=v_0-u_0`

`\Rightarrow 12=v_0-2.5`

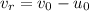
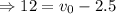
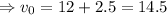`\Rightarrow v_0=12+2.5=14.5` m/s

Hence, the boat's speed relative to the ground when it is heading east, with the current, is 14.5 m/s.

(b) When the boat is heading toward the west (in the opposite direction of the current of the river)

The relative velocity,
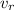`v_r`, of the boat with respect to ground is

`v_r=v_0-(-u_0)`

`\Rightarrow 12=v_0+2.5`

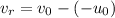
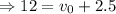
`\Rightarrow v_0=12-2.5=9.5` m/s

Hence, the boat's speed relative to the ground when it is heading west, against the current, is 9.5 m/s.