Question

In a casino in Blackpool there are two slot machines (machine 1 and machine 2): one that pays out 10 % of the time, and one that pays out 20 % of the time. Obviously, you would like to play on the machine that pays out 20% of the time but you do not know which of the two machines is the more generous. You thus adopt the following strategy: you assume initially that the two machines are equally likely to be the generous machine. You then select one of the two machines at random (this turns out to be machine 1) and put a coin into it. Given that you loose that first bet estimate the probability that machine 1 is the more generous of the two machines

What do I know?
What do I want to find out?
What do I expect the answer to be?
How do I go from what I know to what I want to find?
Is the answer consistent with what I expected?

Answer 1

Explanation:

From the given information:

We are told that there exist two machines

Machine 1 and Machine 2

Given that machine 1 pays 10% when it is generous, then the probability can be computed as:

P(pays | machine 1 is generous) = 0.10

Also, machine 2 pays 20% when it is generous, then the probability that the machine pays 20% when it is generous is :

P(pays | machine 2 is generous) = 0.20

However, the two machines have an equal chance of being generous.

Therefore, the probability that machine 1 is generous is equal to the probability that machine 2 is also generous.

i.e.

P( machine 1 is generous) = P( machine 2 is generous) = 0.50

The first objective is to find the probability that the machine 1 is generous, given that the player loses the first bet.

i.e. P (machine 1 is generous | but lost)

Thus, we know that the probability that the machine is generous is = 0.5, therefore, the probability that the machine is generous is 50% when he loses the first bet.

Therefore, to find the probability that the machine 1 is generous | but lost, we have:

`\mathbf lost) = (P(machine \ 1 \ is \ generous \ \cap lost ))/(P(lost))`

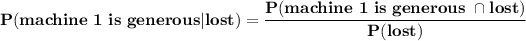
Let:

P(lost | machine 1 is generous) = A

P(machine 1 is generous) = B

P (Pays | machine 1 is generous ) = C

P(Pays | machine 2 is generous ) = D

P(machine 2 is generous) = E

`\mathbf lost) = ((1 - C) * B)/( (1 - C) * B + (1 - D) * E)`

`\mathbfP(machine \ 1 \ is \ generous`

`\mathbfP(machine \ 1 \ is \ generous`

`\mathbf lost) =0.5294`

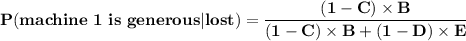
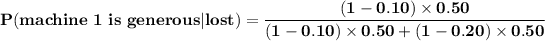
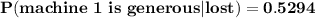
Thus, the probability that machine 1 loses the first bet but it is generous = 0.5294

Thus, since the answer is close to 0.50, we say that the answer is consistent with what is expected.