Answer:
(a). The rocket's velocity is 117.6 m/s.
(b). The rocket can reach at maximum height is 940.8 m.
(c). The velocity the instant before the rocket crashes on the ground is 135.7 m/s.
Explanation:
Given that,
Acceleration = 29.4 m/s²
Time = 4 sec
(a). We need to calculate the rocket's velocity
Using equation of motion

Put the value into the formula

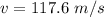
We need to calculate the maximum height at the moment fuel ends
For the value of x₁
Using equation of motion
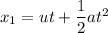
Put the value into the formula
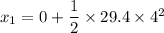
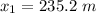
We need to calculate the value of x₂
Using equation of motion
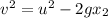
Put the value into the formula
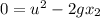
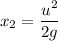
Put the value in to the formula
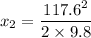
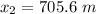
(b). We need to calculate the maximum this rocket can reach
Using formula for height
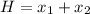
Put the value into the formula
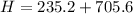
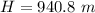
(c). We need to calculate the velocity the instant before the rocket crashes on the ground
Using equation of motion
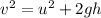
Put the value into the formula

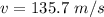
Hence, (a). The rocket's velocity is 117.6 m/s.
(b). The rocket can reach at maximum height is 940.8 m.
(c). The velocity the instant before the rocket crashes on the ground is 135.7 m/s.