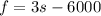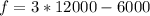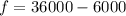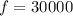Answer:
First year = 30000
Second year = 12000
Explanation:
Given
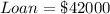
Represent first year with f and second year with s.
So, we have:
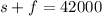
and
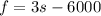
Required
Solve for f and S
Substitute 3s - 6000 for f in the first equation.
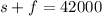
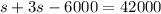
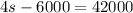
Collect Like Terms
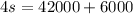
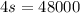
Solve for s
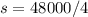
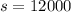
Substitute 12000 for s in