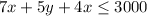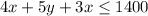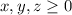Question

A furniture company is producing three types of furniture. Product A requires 7 board feet of wood and 4 lbs of wicker. Product B requires 5 board feet of wood and 5 lbs of wicker. Product C requires 4 board feet of wood and 3 lbs of wicker. There are 3000 board feet of wood available for product and 1400 lbs of wicker. Product A earns a profit margin of $35 a unit, Product B earns a profit margin of $42 a unit, and Product C earns a profit margin of $20 a unit. Formulate the problem as a linear program.

Answer 1

Given:

Product A requires 7 board feet of wood and 4 lbs of wicker.

Product B requires 5 board feet of wood and 5 lbs of wicker.

Product C requires 4 board feet of wood and 3 lbs of wicker.

Available wood = 3000 board feet

Available wicker = 1400 lbs

Profit margin of A = $35 per unit

Profit margin of B = $42 per unit

Profit margin of C = $20 per unit

To find:

The linear programming problem for given situation.

Solution:

Let the number of units produced of products A, B and C are x, y and z respectively.

Product A Product B Product C Total

Board feet of wood 7 5 4 3000

wicker 4 5 3 1400

Objective function: Maximize
`z=35x+42y+20z`

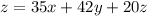
s.t.,

Board feet of wood :
`7x+5y+4x\leq 3000`

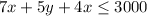
Wicker :
`4x+5y+3x\leq 1400`

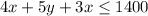
Number of units cannot be negative. So,
`x,y,z\geq 0`.

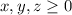Therefore, the required LPP is

Maximize
`z=35x+42y+20z`

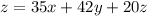
s.t.,

`7x+5y+4x\leq 3000`

`4x+5y+3x\leq 1400`

`x,y,z\geq 0`