Question

A scientist needs 10 liters of a 20% acid solution for an experiment, but she has only a 5% solution and a 40% solution. To the nearest tenth of a liter, about how many liters of the 5% and the 40% solutions should she mix to get the solution she needs? Write and solve an equation to match the situation.

Answer 1

5% solution needed = 5.7 liters

40% solution needed = 4.3 liters

Explanation:

Let the amount of 5% solution is needed = x liters

And the amount of 40% solution is needed = y liters

Concentration of the final solution = 20%

5x + 40y = 20(x + y)

x + 8y = 4(x + y)

4y = 3x

x =
`(4)/(3)y` -------(1)

Total volume of the final solution needed = 10 liters

Therefore, x + y = 10 --------(2)

Now substitute the value of x from equation (1) to equation (2).

`(4)/(3)y+y=10`

`(7)/(3)y=10`

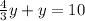
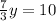
y = 4.3 liters

From equation (2),

x + 4.3 = 10

x = 5.7 liters