Question

Look at the triangle show on the right. The Pythagorean Theorem states that the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse. Margaret uses this theorem to simplify and rewrite the expression (b/r)^2 + (a/r)^2 using the triangle shown. Which trigonometric identity can she prove with her expression? *

Answer 1

`cos^2\theta + sin^2\theta = 1`

Explanation:

Given

`((b)/(r))^2 + ((a)/(r))^2`

Required

Use the expression to prove a trigonometry identity

The given expression is not complete until it is written as:

`((b)/(r))^2 + ((a)/(r))^2 = ((r)/(r))^2`

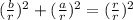
Going by the Pythagoras theorem, we can assume the following.

• a = Opposite
• b = Adjacent
• r = Hypothenuse

So, we have:

`Sin\theta = (a)/(r)`

`Cos\theta = (b)/(r)`

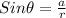
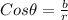
Having said that:

The expression can be further simplified as:

`((b)/(r))^2 + ((a)/(r))^2 = 1`

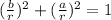
Substitute values for sin and cos

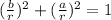`((b)/(r))^2 + ((a)/(r))^2 = 1` becomes

`cos^2\theta + sin^2\theta = 1`