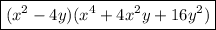Answer:
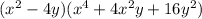
Explanation:
Factoring
We need to recall the following polynomial identity:
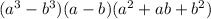
The given expression is:
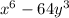
To factor the above expression, we need to find a and b, knowing a^3 and b^3. a is the cubic root of a^3, and b is the cubic root of b^3:
![a=\sqrt[3]{x^6}=x^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/tmfbk7lkitksoqgikqw8ips10e5de54uyc.png)
![b=\sqrt[3]{64y^3}=4y](https://img.qammunity.org/2021/formulas/mathematics/high-school/w03q4so051lo0zl61j9v4l690fwo0i39o2.png)
Now we apply the identity:
![x^6– 64y^3=(x^2-4y)[(x^2)^2+(x^2)*(4y)+(4y)^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vfjy0av9q0ldghlqlqi7kv2ywt9q54sf8n.png)
Operating:
![x^6– 64y^3=(x^2-4y)[x^4+4x^2y+16y^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/oa6itxgjuzbzxsizgye6fa6qsj18c62w3g.png)
The remaining factors cannot be factored in anymore. Thus the completely factored form is: