Question

How do you solve this? Without going into anything to complicated as this should be Year 10 maths

Answer 1

Given : ABCD is a square with each side 5cm .

To Find : The area of the shaded region .

Solution : On observing the figure we can see two quadrants , quadrant ADC & quadrant ABC .

If we join A to C , then it will be common for triangles ADC & ABC . And they will be congruent by SSS congruence condition.

Therefore the area of both quadrants will also be equal . Now we can find area of quadrant as ;

`\large\boxed{\red{\bf Area_(quadrant)=(\pi r^2)/(4)}}`

Here radius will be equal to 5cm .

⇒ Area = πr² / 4 .

⇒ Area = π (5cm)² / 4 .

⇒ Area = 22/7 × 25 × 4 cm².

⇒ Area = 19.64 cm² .

So , total area of both quadrants = 39.28 cm² .

Also , area of square will be :

`\large\boxed{\bf{\red{Area_(square)=(side)^2}}}`

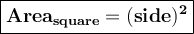
⇒ Area = 5cm × 5cm .

⇒ Area = 25 cm².

Now , subtract area of one quadrant from the area of square = 25cm² - 19.64 cm² = 5.36 cm².

Similarly area of other white region = 5.36cm² .

And the areas sum will be = 5.36cm² × 2 = 10.72cm² .

Now , from the figure it's clear that ,

⇒ Area of unshaded region + Area of shaded region = 25cm².

⇒ 10.72cm² + ar( Shaded region ) = 25cm².

⇒ ar ( Shaded region ) = 25cm² - 10.72cm².

⇒ ar ( Shaded region ) = 14.28 cm².

Hence the area of shaded region is 14.28 cm².

`\large\boxed{\red{\bf Answer = 14.28cm^2}}`