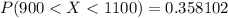Question

The annual gas bill for a town household are considered to be normally distributed with a mean of $ 1130 and a standard deviation of $ 150. If one household is randomly selected, what is the probability that the gas bill will be between $900 and $1100?

Answer 1

The probability is
`P(900 < X < 1100) = 0.358102`

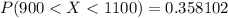
Explanation:

From the question we are told that

The population mean is
`\mu = \$ 1130`

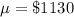
The standard deviation is
`\sigma = \$ 150`

Generally the probability that the gas bill will be between $900 and $1100 is mathematically represented as

`P(900 < X < 1100) = P((900 - 1130 )/(150 ) < (X - \mu)/(\sigma ) < (1100 - 1130 )/(150 ) )`

=>
`P(900 < X < 1100) = P(-1.533 < (X - \mu)/(\sigma ) < -0.2 )`

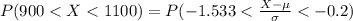
Generally
`(X - \mu)/(\sigma ) = Z (The\ standardized \ value \ of \ X)`

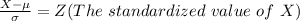
So

`P(900 < X < 1100) = P(-1.533 < Z< -0.2 )`

`P(900 < X < 1100) = P( Z< -0.2 ) - P(Z < -1.533)`

From the z table

`P(Z < -0.2 ) = 0.42074`

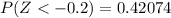
and

`P(Z < -1.533) = 0.062638`

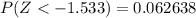
So

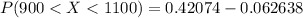
`P(900 < X < 1100) = 0.42074 - 0.062638`

=>
`P(900 < X < 1100) = 0.358102`