Question

The probability that a truck will be going over the speed limit on I-77 South between Dobson and Elkin is about 75%. Suppose a random sample of five trucks are observed on this stretch of I-77. a. Find the mean of this probability distribution. Show the formula and your work. b. Interpret the mean in the context of the problem. c. Find the standard deviation of this probability distribution. Round your answer to 2 decimal places. d. Find the probability that exactly 3 of the observed trucks are speeding. e. Find the probability that less than 3 of the observed trucks are speeding.

Answer 1

Explained below.

Explanation:

Let X = number of trucks that will be going over the speed limit on I-77 South between Dobson and Elkin.

The probability of X is, p = 0.75.

A random sample of n = 5 trucks are observed on this stretch of I-77.

The random variable X follows a binomial distribution with parameters n = 5 and p = 0.75.

(a)

Compute the mean as follows:

`\mu=n* p=5* 0.75=3.75`

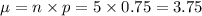
The mean of this probability distribution is 3.75.

(b)

The mean of 3.75 implies that on average 3.75 trucks that will be going over the speed limit on I-77 South between Dobson and Elkin.

(c)

Compute the standard deviation as follows:

`\sigma=√(np(1-p))=√(5* 0.75* (1-0.75))=0.968`

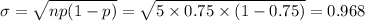
Thus, the standard deviation of this probability distribution is 0.97.

(d)

Compute the probability that exactly 3 of the observed trucks are speeding as follows:

`P(X=3)={5\choose 3}(0.75)^(3)(1-0.75)^(5-3)\\\\=10* 0.421875* 0.0625\\\\=0.263671875\\\\\approx 0.2637`

Thus, the probability that exactly 3 of the observed trucks are speeding is 0.2637.

(e)

Compute the probability that less than 3 of the observed trucks are speeding as follows:

`P(X<3)=P(X=0)+P(X=1)+P(X=2)\\\\=\sum\limits^(2)_(x=0){{5\choose x}(0.75)^(x)(1-0.75)^(5-x)}\\\\=0.0009765625+0.0146484375+0.087890625\\\\=0.103515625\\\\\approx 0.1035`

Thus, the probability that less than 3 of the observed trucks are speeding is 0.1035.