Given:
Total of raffle tickets = 30
Number of tickets Jason bought = 10
Number of prizes = 3
To find:
The probability that Jason will win all 3 of the prizes if once a raffle ticket wins a prize it is thrown away.
Solution:
Total of raffle tickets = 30
Number of prizes = 3
So, number of total outcomes is
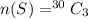
Number of tickets Jason bought = 10
So, number of favorable outcomes is
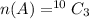
Now,
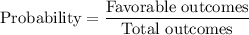
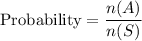
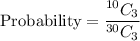
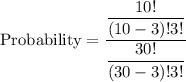
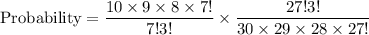
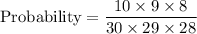

Therefore, the correct option is A.