Question

At New years you decide to join a gym to lose all those calories gained during winter break and youre comparing two different gyms. The first gym, gym A has a 12$ initiation fee and then costs 10$ per month. The second gym , gym B has a 20$ initiation fee and then costs 6$ per month. Create an equation that aims to find when these two gyms will cost the same amount of money

Answer 1

Given:

For gym A, initiation fee = $12 and cost = $10 per month.

For gym B, initiation fee = $20 and cost = $6 per month.

To find:

The equation that aims to find when these two gyms will cost the same amount of money,

Solution:

Let the number of months be x.

Cost function = Initiation fee + (cost)(x)

Cost function for gym A is

`f(x)=12+10x`

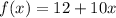
Cost function for gym B is

`g(x)=20+6x`

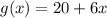
Cost of these two gyms are equal if f(x)=g(x).

`12+10x=20+6x`

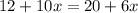
Therefore, the required equation is
`12+10x=20+6x`.

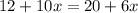On solving this equation, we get

`10x-6x=20-12`

`4x=8`

`x=2`

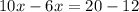
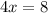
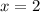
Hence, after 2 months the cost of these two gyms are same.