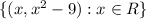1 Answer

Fiya · Answer 1 · 2023-06-10T14:16:18+0000

Here's the Solution to this Question

Given A
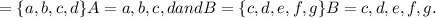
$= \{a,b,c,d\}A={a,b,c,d} and B = \{c,d,e,f,g\}B={c,d,e,f,g} .$

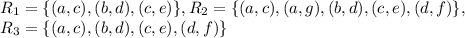
$R_1 = \{(a,c), (b,d), (c,e)\}, R_2 = \{(a,c), (a,g), (b,d), (c,e), (d,f)\}, \\ R_3 = \{(a,c), (b,d), (c,e), (d,f)\}$

A relation is a function when every element of set A has image in B and a element of set A can-not have more than one image in set B.

So, Relation
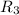R_3 is a function.

(c) Given
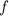is a real valued function defined by
f(x) = x^2 - 9 .

(I) Function is defined for all real values of
. Hence,

Domain of
f=R

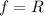
(ii) Now, as
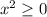
$x^2 \geq 0$
$\implies$
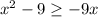
$x^2-9 \geq -9x$

Hence, Range of f=[−9,∞)

(iii) Representation of
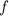as a set of ordered pair =
$\{ (x,x^2-9) : x \in R\}$