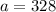Answer:
328
Explanation:
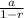 is the equation for the sum of an infinite geometric series, where
is the equation for the sum of an infinite geometric series, where
 is the first term of the infinite geometric series, and r is the common ratio between the terms. Here, we can find the common ratio between any consecutive terms.
is the first term of the infinite geometric series, and r is the common ratio between the terms. Here, we can find the common ratio between any consecutive terms.
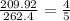
Therefore,
 .
.
This simplifies to
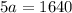
Therefore,