Question

This table gives a few (x, y) pairs of a line in the coordinate plane. What is the x-intercept of the line?

Answer 1

x=-14

Explanation:

The x-intercept of a line is the value of x that makes y=0.

A line can be expressed in its slope-intercept form:

y=mx+b

Once determined the equation of the line, the x-intercept can be calculated by setting y=0 and solving for x.

Let's find the slope of the line.

Suppose we know the line passes through two points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

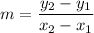
Let's pick the first two points of the table (-94,24) (-74,18). The slope is:

`\displaystyle m=(18-24)/(-74+94)=(-6)/(20)=-(3)/(10)`

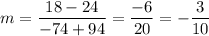
The equation of the line is:

`\displaystyle y=-(3)/(10)x+b`

Now use one of the points to find b, for example (-94,24):

`\displaystyle 24=-(3)/(10)\cdot (-94)+b`

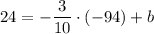
Operating:

`\displaystyle 24=(141)/(5)+b`

Solving:

`b=24-(141)/(5)=-(21)/(5)`

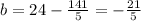
The complete equation of the line is:

`\displaystyle y=-(3)/(10)x-(21)/(5)`

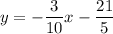
To find the x-incercept, set y=0 and solve:

`\displaystyle 0=-(3)/(10)x-(21)/(5)`

`\displaystyle x=((21)/(5))/(-(3)/(10))=-(21)/(5)\cdot (10)/(3)`

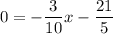
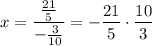
x=-14