second question: How many seconds after the first snowball
should you throw the second so that they
arrive on target at the same time?
Answer in units of s.
Answer:
Part 1: 28°
Part 2: 1.367
Step-by-step explanation:
Part 1:
Given: 62°
Simple
θ = 90°- 62°
θ = 28°
Part 2:
Y-direction
Δy
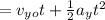
![0=[16.2sin(62)]t_(1)+1/2(-9.8)t_(1)^(2) \\](https://img.qammunity.org/2021/formulas/physics/college/o7p71ixvbmtrcoytvyyt70x4sq02jahocl.png)
![t_(1) =(2[16.2sin(62)])/(9.8)](https://img.qammunity.org/2021/formulas/physics/college/wd608eonfywosvuwa0nmah780joweq882r.png)
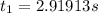
![0=[16.2sin(28)]t_(2)+1/2(-9.8)t_(2)^(2)](https://img.qammunity.org/2021/formulas/physics/college/ueguz6kotma3p4i39nhzvzqjc0h887ldb6.png)
![t_(2) =(2[16.2sin(28)])/(9.8)](https://img.qammunity.org/2021/formulas/physics/college/5u4xcr90bqzbs8xt36hjge50biqeczhvau.png)
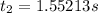
Δt
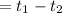
Δt
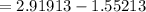
Δt= 1.367s
Hope it helps :)