Question

What is the value of a?

Enter your answer in the box. Enter your answer as a simplified fraction.

Answer 1

Answer: a = -5/2

==========================================

Work Shown:

The scalar (2/5a+6) multiplies with the matrix on the left side to get the matrix on the right side

So this is what your steps could look like

`((2)/(5)a+6)\begin{bmatrix}3 \\ -2 \\ 7\end{bmatrix}=\begin{bmatrix}15 \\ -10 \\ 35\end{bmatrix}\\\\\\\begin{bmatrix}((2)/(5)a+6)*3 \\ ((2)/(5)a+6)*(-2) \\ ((2)/(5)a+6)*7\end{bmatrix}=\begin{bmatrix}15 \\ -10 \\ 35\end{bmatrix}\\\\\\`

`\begin{bmatrix}(2)/(5)a*3+6*3 \\ (2)/(5)a*(-2)+6*(-2) \\ (2)/(5)a*7+6*7\end{bmatrix}=\begin{bmatrix}15 \\ -10 \\ 35\end{bmatrix}\\\\\\\begin{bmatrix}(6)/(5)a+18 \\ -(4)/(5)a-12 \\ (14)/(5)a+42\end{bmatrix}=\begin{bmatrix}15 \\ -10 \\ 35\end{bmatrix}\\\\\\`

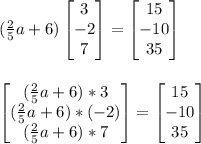
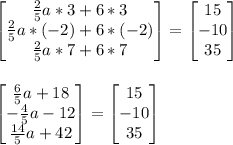
The last matrix equation leads to this system of equations

`\begin{cases}(6)/(5)a+18=15 \\ -(4)/(5)a-12=-10 \\ (14)/(5)a+42=35\end{cases}\\\\\\`

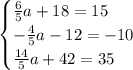
If we pick any of those equations, and solve for 'a', then we'll get our answer.

---------------------

Let's say we pick the first equation

(6/5)a+18 = 15

(6/5)a = 15-18

(6/5)a = -3

a = -3(5/6)

a = -15/6

a = -5/2

--------------------

If we pick on the second equation, then,

(-4/5)a-12 = -10

(-4/5)a = -10+12

(-4/5)a = 2

a = 2(-5/4)

a = -10/4

a = -5/2

--------------------

Or we could solve the third equation for 'a'

(14/5)a+42 = 35

(14/5)a = 35-42

(14/5)a = -7

a = -7*(5/14)

a = -35/14

a = -5/2

-------------------

You only need to solve one equation to find 'a', though it's good practice to solve all three to see all three rows agreeing with one another.