Explanation:
You can write an equation of a line conveniently by point-slope form. It's in the form of
 where
where
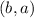 is the coordinates of a point that's on the line and
is the coordinates of a point that's on the line and
 is the slope of the line.
is the slope of the line.
Now choose a point (It doesn't really matter which one) and plug that in the equation. I'll choose
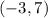 where
where
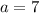 and
and
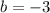
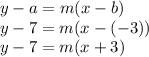
The next thing we have to do now is finding the slope,
 , where it's equal to
, where it's equal to
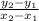 . I'll make
. I'll make
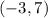 point 1 and
point 1 and
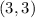 point 2.
point 2.
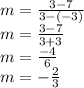
Now let's plug that to our equation.
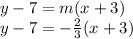
Now we have the equation but out of all the choices it seemed that all of them are in slope-intercept form all you have to do now is make our equation rewrite it in slope-intercept form.
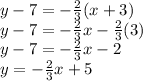
Answer:
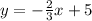 is your equation.
is your equation.