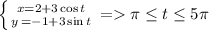Question

How do you do this question?

Answer 1

`\left \{ {{x=2+3\cos t} \atop {y\:=-1+3\sin t}} \right. => \pi \leq t \leq 5\pi`

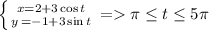
Explanation:

The standard equation of a circle centered at (a,b) with radius r would be (x - a)^2 + (y - a)^2 = r^2

This example represents a circle with center (2, - 1) having a radius of 3

The parametric equation of a circle centered at (0,0) would be;

x = r cos t,

y = r sin t

And so when centered at (a, b) we would have;

x = a + r cos t,

y = b + r sin t

In this case x = 2 + 3 cos t, and y = - 1 + 3 cos t

Now if the particle starts at (-1, - 1), correspondent to a start parameter of t = π, we need two revolutions so it should be that t = π + 2 * 2π = 5π.

`\left \{ {{x=2+3\cos t} \atop {y\:=-1+3\sin t}} \right. => \pi \leq t \leq 5\pi`