Question

Jill is building a wooden raised bed garden for her vegetable she wants the frame to have dimension X feet by X +3 feet if she wants the garden to have a maximum area of 50 ft.² what are the possible values of X

Answer 1

Answer: 0ft < X ≤ 5.73ft

Explanation:

In this case, we have a rectangle.

For a rectangle of length L and width W, the area is:

A = L*W.

And we have:

L = X

W = X + 3ft.

Then the area will be:

A = X*(X + 3ft) = X^2 + 3ft*X.

And we want to have a maximum area of 50ft^2.

Then we can write:

A = X^2 + 3ft*X ≤ 50ft^2

Now let's solve this for X.

Now, the first thing we can see is that both coefficients in our quadratic equation are positive, so as the absolute value of X increases, also does the whole equation.

Then makes sense start for the upper limit of X, this is when:

X^2 + 3ft*X = 50ft^2.

Now we can solve the quadratic equation:

X^2 + 3ft*X - 50ft^2 = 0

Applying the Bhaskara formula, the solutions are:

`X = (-3ft +- √((3ft)^2 - 4*1*(-50ft^2)) )/(2) = (-3ft +-14.46ft )/(2)`

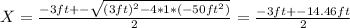
Then we have two solutions:

X = (-3ft - 14.46ft)/2 = -8.73 ft.

X = (-3ft + 14.46ft)/2 = 5.73 ft

Because X represents a distance, it can only be positive, then we must select the option X = 5.73ft.

This is the maximum value of X, and we will have:

0ft < X ≤ 5.73ft

Where the lower limit is there because we can not have X = 0ft, as this does not have physical meaning.