Question

Sam invests a sum of money in a retirement account with a fixed annual interest rate of 7%

compounded quarterly. After 13 years, the balance reaches $19,280.02. What was the amount of
the initial investment? ROUND YOUR ANSWER TO THE NEAREST DOLLAR (do NOT put a dollar
sign $ in your answer)

Answer 1

The initial amount of investment was $7,822

Explanation:

The formula for compound interest, including principal sum is:

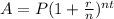`A=P(1+(r)/(n))^(nt)`, where

• A is the future value of the investment/loan, including interest

• P is the principal investment amount

• r is the annual interest rate (decimal)

• n is the number of times that interest is compounded per unit t

• t is the time the money is invested or borrowed for

Let us use this rule to solve the question

∵ Sam invests a sum of money in a retirement account with a fixed

annual interest rate of 7% compounded quarterly

∴ r = 7% =
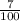`(7)/(100)` = 0.07

∴ n = 4 ⇒ compounded quarterly

∵ After 13 years, the balance reaches $19,280.02

∴ A = 19,280.02

∴ t = 13

Substitute these values in the rule above to find P

∵
`19,280.02=P(1+(0.07)/(4))^(4(13))`

∴
`19,280.02=P(1.0175)^(52)`

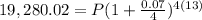
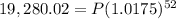
→ Divide both sides by
`(1.0175)^(52)`

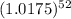
∴ 7,821.99888 = P

→ Round it to the nearest dollar

∴ 7,822 = P

∴ P = $7,822

∴ The initial amount of investment was $7,822.