Hey there,
The squeeze theorem shows if
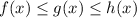 for all real numbers
for all real numbers
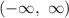 then f(x) = h(x) but g(x) has to equal that as well.
then f(x) = h(x) but g(x) has to equal that as well.
Let's say we have [
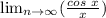 ]
]
~Apply the theorem
Note that [
 ] and [
] and [
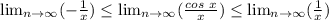 ]
]
~Apply the infinity property to every side but the middle
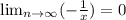

So...
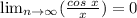
Best of Luck!