Question

A line passes through the points (-6, 4) and (-2, 2). Which is the equation of the line?

O y--3x+1
O y-5x+7
O y = -2x - 8
O y = 2x + 16

Answer 1

`\displaystyle y=-(1)/(2)x+1`

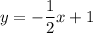
Explanation:

The equation of any line in slope-intercept form is:

y=mx+b

Being m the slope and b the y-intercept.

Assume we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:

`\displaystyle m=(y_2-y_1)/(x_2-x_1)`

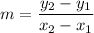
Two points are given: (-6,4) and (-2,2). Calculating the slope:

`\displaystyle m=(2-4)/(-2+6)=(-2)/(4)=-(1)/(2)`

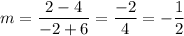
The equation of the line is, so far:

`\displaystyle y=-(1)/(2)x+b`

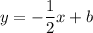
To calculate the value of b, we use any of the given points, for example (-6,4):

`\displaystyle 4=-(1)/(2)(-6)+b`

`\displaystyle 4=3+b`

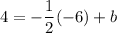
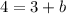
Solving:

b = 1

The equation of the line is:

`\boxed{\displaystyle y=-(1)/(2)x+1}`

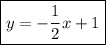
We can see none of the choices is correct.