Answer:
3) 670.7 °C (nearest tenth)
4) 818.2 torr (nearest tenth)
Step-by-step explanation:
Question 3
Charles's Law

where:
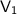 = initial volume
= initial volume
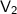 = final volume
= final volume
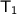 = initial temperature
= initial temperature
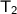 = final temperature
= final temperature
Given values:
Convert the temperature in Celsius to kelvin by adding 273.15:
⇒
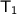 = 10 + 273.15 = 283.15 K
= 10 + 273.15 = 283.15 K
Substitute the given values into the formula and solve for T₂:
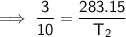
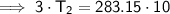
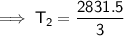
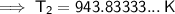
Converting kelvins back to Celsius:
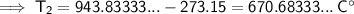
Therefore, the final temperature will be 670.7 °C (nearest tenth).
Question 4
Gay-Lussac's Law

where:
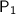 = initial pressure
= initial pressure
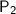 = final pressure
= final pressure
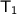 = initial temperature
= initial temperature
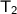 = final temperature
= final temperature
Given values:
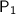 = 760 torr
= 760 torr-
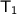 = 27°C
= 27°C
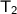 = 50°C
= 50°C
Convert the temperature in Celsius to kelvin by adding 273.15:
⇒
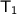 = 27 + 273.15 = 300.15 K
= 27 + 273.15 = 300.15 K
⇒
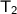 = 50 + 273.15 = 323.15 K
= 50 + 273.15 = 323.15 K
Substitute the given values into the formula and solve for P₂:
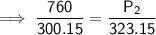
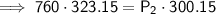
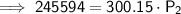
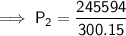
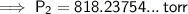
Therefore, the new pressure is 818.2 torr (nearest tenth).