Question

The straight line 4x+5y-20 = 0 cuts the X-intercept, Y-intercept and hence find area of traingleAOB​

Answer 1

The area of the triangle AOB is 10

Explanation:

The line 4x+5y-20=0 forms a triangle AOB as shown in the figure below. The points A and B are the y-intercept and x-intercept respectively, and the point O is the origin.

To find the intercepts, we set the other variable to zero and solve the resulting equation.

Set x=0, the y-intercept is found as follows:

4(0)+5y-20=0

5y=20

y=20/5=4

The y-intercept is y=4

Set y=0, the x-intercept is now found:

4x+5(0)-20=0

4x=20

Solve:

x=20/4=5

The x-intercept is x=5

Now, knowing the base b and the height of the triangle h are 5 and 4 respectively, the area of the triangle is:

`\displaystyle A=(bh)/(2)`

`\displaystyle A=(5\cdot 4)/(2)=10`

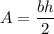
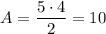
The area of the triangle AOB is 10