Answer:
The ball lands on the ground at t=2.55 seconds
Explanation:
Quadratic Equation
The following function models the height above the ground of a ball hit into the air at time t seconds:
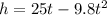
We need to find the value of t when the ball hits the ground.
At ground level, h is zero, thus:
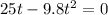
This is an incomplete quadratic equation that can be easily solved by factoring:
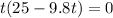
There are two solutions:
t=0
t=25/9.8=2.55 s
The first solution corresponds to the moment when the ball is hit, and the second is when it returns to the ground, thus:
The ball lands on the ground at t=2.55 seconds